Tham lam là một trong những phương pháp phổ biến nhất để thiết kế giải thuật. Rất nhiều thuật toán nổi tiếng được thiết kế dựa trên tư tưởng của tham lam, ví dụ như thuật toán tìm đường đi ngắn nhất của Dijkstra, thuật toán cây khung nhỏ nhất của Kruskal, v.v. Trong bài này chúng ta sẽ tìm hiểu phương pháp thiết kế giải thuật này.
Lưu file trên đĩa từ
Bài toán như sau:
$C(\pi(i)) = \sum_{i=1}^{k} L[\pi(k)] $
Tìm cách lưu trữ file sao cho việc truy xuất được hiệu quả nhất, biết rằng các file có xác suất truy cập như nhau.
Vì các file có xác suất truy cập như nhau, với một cách lưu trữ $\pi$ cho trước, chi phí để truy xuất ngẫu nhiên một file có kì vọng là:
$E[cost_{\pi}] = \frac{\sum_{i=1}^n C(\pi(i))}{n} = \frac{\sum_{i=1}^n \sum_{k=1}^i L[\pi(k)]}{n}$
Cách lưu trữ file mà chúng ta có thể nghĩ đến ngay đó là các lưu các file nhỏ ở đầu đĩa từ và lưu các file lớn ở cuối đĩa từ. Vấn đề còn lại là chứng minh rằng cách lưu này là một cách lưu file tối ưu ($E[cost_{\pi}]$ nhỏ nhất).
Chứng minh: Giả sử tồn tại một cách lưu trữ tối ưu $\pi$ và chỉ số $i$ sao cho $L[\pi(i)] > L[\pi(i+1)]$. Gọi $\pi'$ là hoán vị thu được từ $\pi$ bằng cách đổi chỗ $L[\pi(i)]$ và $L[\pi(i+1)]$. Ta có:
$\begin{array} {lcl} E[cost_{\pi}] - E[cost_{\pi'}] & = & \frac{C(\pi(i)) + C(\pi(i+1)) - C(\pi'(i)) - C(\pi'(i+1))}{n} \\ & = & \frac{L[\pi(i)] - L[\pi(i+1)]}{n} > 0 \end{array}$
Do đó, $E[cost_{\pi}] > E[cost_{\pi'}]$, trái với giả thiết $\pi(i)$ là cách lưu trữ tối ưu.
Theorem 1 cho chúng ta một giải thuật tham lam giải bài toán lưu trữ file như sau:
$S \leftarrow \{1,2,\ldots,n\}$
repeat
choose $s \in S$ with minimum $L[s]$
write $s$ to the tape
$S \leftarrow S \setminus \{s\}$
until $S = \emptyset$
Bằng cách sắp xếp theo chiều tăng của kích thước file, chúng ta có thể thực thi thuật toán trên trong thời gian $O(n\log n)$. Bây giờ chúng ta hãy thay đổi bài toán một chút như sau:
$C(\pi(i)) =F[\pi(i)] \sum_{i=1}^{k} L[\pi(k)] $
Tìm cách lưu trữ file sao cho việc truy xuất được hiệu quả nhất.
Với bài toán này, tổng chi phí để truy xuất file là:
$Cost_{\pi} = \sum_{i=1}^n F[\pi(i)] \sum_{k=1}^iL[\pi(k)]$
Ta sẽ tổng quát hóa thuật toán ở Problem 1 như sau: lưu file theo tỉ lệ $L[i]/F[i]$ tăng dần. Ta sẽ chứng minh rằng cách lưu file này có tổng chi phí nhỏ nhất:
Chứng minh: Tương tự như chứng minh ở Theorem 1, ta giả sử tồn tại một cách lưu trữ tối ưu $\pi$ và chỉ số $i$ sao cho $\frac{L[\pi(i)]}{F[\pi(i)]} \leq \frac{L[\pi(i+1)]}{F[\pi(i+1)]}$. Gọi $\pi'$ là hoán vị thu được từ $\pi$ bằng cách đổi chỗ $L[\pi(i)]$ và $L[\pi(i+1)]$. Ta có:
$\begin{array} {lcl} Cost_{\pi} - Cost_{\pi'} & = & F[\pi(i)]C(\pi(i)) + F[\pi(i+1)]C(\pi(i+1)) - F[\pi'(i)]C(\pi'(i)) - F[\pi'(i+1)]C(\pi'(i+1))\\ & = & F[\pi(i+1)]L[\pi(i)] - F[\pi(i)]L[\pi(i)] \\ & > & 0 \qquad \mbox{Since }\frac{L[\pi(i)]}{F[\pi(i)]} \leq \frac{L[\pi(i+1)]}{F[\pi(i+1)]} \end{array}$
Do đó, $Cost_{\pi} > Cost_{\pi'}$, trái với giả thiết $\pi(i)$ là cách lưu trữ tối ưu.
Theorem 2 cho chúng ta một giải thuật tham lam sau:
$S \leftarrow \{1,2,\ldots,n\}$
repeat
choose $s \in S$ with minimum $\frac{L[s]}{F[s]}$
write $s$ to the tape
$S \leftarrow S \setminus \{s\}$
until $S = \emptyset$
Ta xét bài toán phức tạp hơn sau:
Bài toán chọn môn học
Ví dụ: ở hình dưới đây (lấy từ [1]), mỗi môn học được biểu diễn bởi một thanh ngang có chiều dài $F[i]-S[i]$. Tập các thanh màu xanh chính là một tập có số lượng lớn nhất các môn học không gối lên nhau:

Bài toán này có thể giải bằng phương pháp quy hoạch động với thời gian $O(n^2)$. Chi tiết coi như bài tập cho bạn đọc. Ở đây mình đưa ra cách giải bằng phương pháp tham lam. Có 3 cách lựa chọn lớp học tham lam mà bạn có thể nghĩ đến:
- Chọn lớp học bắt đầu sớm nhất trước. Tuy nhiên bạn có thể nghĩ ngay đến vấn đề của các chọn này là nếu có một lớp học bắt đầu sớm nhất nhưng lại kéo dài rất lâu thì bạn chỉ có thể chọn được 1 lớp học
- Chọn lớp học ngắn nhất trước. Vấn đề của các chọn này là nếu có một lớp học ngắn nhưng gối lên các lớp học bắt đầu trước và sau lớp học này, bạn sẽ không thể có phương án tối ưu. Ta có thể dễ dàng nghĩ ra phản ví dụ của cách chọn này chỉ với 3 lớp học
- Chọn lớp học có thời gian hoành thành sớm nhất trước. Có vẻ đây là một cách chọn tham lam tốt vì nếu chọn lớp hoàn thành sớm nhất trước, bạn sẽ có nhiều thời gian còn lại để chọn các lớp học khác. Thực tế đây là một cách chọn tham lam cho bạn phương án tối ưu.
Thuật toán như sau:
sort $F$ in increasing order
permute indices of $S$ to match $F$
$J \leftarrow \{1\}$
tmp $\leftarrow $1
for $i \leftarrow 2 $ to $n$
if $F[tmp] \leq S[i]$ [[class $i$ does not confict with tmp]]
tmp $\leftarrow$ i
$J \leftarrow J \cup \{i\}$
return $J$
Code của giả mã bằng C:
#define MAX 1000000
typedef struct { // use struct to keep track of indices
int id;
int s;
int f;
} course;
course A[MAX];
int X[MAX];
int greedy_class_selection(int n){
qsort(A, n, sizeof(*A), compare_finish); // sort courses by finishing time
int i = 0;
int count = 0;
X[0] = 0;
for(i = 1; i < n; i++){
if(A[X[count]].f <= A[i].s){
count++;
X[count] = i;
}
}
return count+1;
}
int compare_finish(const void *a, const void *b){
course *c_a = (course *)a;
course *c_b = (course *)b;
return c_a->f - c_b->f;
}
Dễ dàng thấy thuật toán trên có thể được thực thi trong thời gian $O(n\log n)$. Việc còn lại của chúng ta là chứng minh thuật toán trên cho chúng ta tập các lớp không gối lên nhau có kích thước lớn nhất.
Chứng minh Giả sử $X = \{x_1,x_2,\ldots, x_k\}$ là tập các lớp học đầu ra của thuật toán tham lam và $Y = \{y_1,y_2,\ldots, y_m \}$ là một phương án tối ưu ($k \leq m$), sắp xếp theo chiều tăng dần của thời gian hoành thành. Gọi $Y_k = \{y_1,y_2,\ldots,y_k\} \subseteq Y$ là tập $k$ phần tử đầu tiên của $Y$. Trong số các phương tối ưu, chọn phương án $Y$ sao cho $|X \cap Y_k|$ là lớn nhất. Nếu $X = Y_k$, ta có $m = k$ vì nếu không, ít nhất một lớp học nữa sẽ được thêm vào $X$. Do đó, $X$ là một phương án tối ưu.
Giả sử $X \not= Y_k$. Suy ra tồn tại $1 \leq i \leq k$ sao cho $y_i \not= x_i$. Ta chọn $i$ nhỏ nhất thỏa mãn $y_i \not= x_i$. Như vậy $y_j = x_j, 1 \leq j \leq i-1$. Do $x_i$ là lớp học có thời gian hoành thành sớm nhất sau khi $x_{i-1}$ đã hoàn thành, thời gian hoành thành của $x_i$ sớm hơn $y_i$. Suy ra $x_{i}$ kết thúc trước khi $y_{i+1}$ bắt đầu. Ngoài ra, $y_i \not\in X$ (chứng minh coi như bài tập cho bạn đọc, xem lời giải trong phần comment).
Xét $Y' = Y \setminus \{y_i\} \cup \{x_i\}$, i.e,
$Y' = \{x_1,x_2,\ldots, x_{i-1}, x_i, y_{i+1}, \ldots, y_m\}$
Dễ thấy, $|Y'| = Y = m$ và các lớp trong $Y'$ không gối lên nhau. Do đó $Y'$ là một phương án tối ưu. Tuy nhiên $|X \cap Y'_k| > |X \cap Y_k|$, trái với cách chọn $Y$ là phương án có $|X \cap Y_k|$ lớn nhất. Do đó, $X$ là phương án tối ưu.
Phương pháp chứng minh bằng phản chứng cho bài toán chọn lớp học cũng là một phương pháp chứng minh phổ biến để chứng minh thuật toán tham lam là tối ưu. Ta có thể rút ra các bước như sau:
- Giả sử lời giải tham lam $X$ là không tối ưu. Chọn lời giải tối ưu $Y$ khác $X$ với $|Y\cap X|$ lớn nhất.
- Xét hai phần tử khác nhau đầu tiên giữa hai lời giải này.
- Chứng minh bằng bằng cách trao đổi hai phần tử khác nhau đầu tiên, ta thu được một lời giải tối ưu khác $Y'$ có $|X\cap Y| > |X \cap Y|$, qua đó, ta thu được phản chứng.
Bạn có thể thử phương pháp trên cho bài toán lưu trữ file trên đĩa từ. Giờ chúng ta thử áp dụng ý tưởng đó vào bài toán sau:
Bài toán lập lịch
Ví dụ bạn có 5 tác vụ với thông tin như sau:
| Job | Profit | Deadline |
| 1 | 100 | 2 |
| 2 | 19 | 1 |
| 3 | 27 | 2 |
| 4 | 25 | 1 |
| 5 | 15 | 3 |
Phương án tối ưu là (theo trình tự thực thi) $\{1,3,5\}$ với tổng tiền thưởng thu được là 142.
Tư tưởng tham lam của bài toán này rất đơn giản như sau: Trong tập các tác vụ chưa được chọn, chọn tác vụ có tiền thưởng lớn nhất nếu tác vụ này vẫn còn thực thi được. Ở đây ta luôn duy trì một danh sách các tác vụ đã chọn và một tác vụ gọi là thực thi được nếu ta thêm tác vụ này vào danh sách đó, vẫn tồn tại một cách thực thi sao cho tất cả các tác vụ được hoàn thành trước thời hạn.
Áp dụng với ví dụ trên, đầu tiên ta chọn tác vụ $1$, sau đó là chọn tác vụ $3$ với trình tự $1,3$. Ứng viên tiếp theo là $4$, tuy nhiên ta không thể thực thi toàn bộ $1,2,4$ trước thời hạn, do đó ta bỏ qua $4$. Tương tự như vậy, tác vụ $2$ cũng không thể được chọn và cuối cùng ta chọn $5$. Như vậy, thuật toán tham lam sẽ cho ta các tác vụ $\{1,3,5\}$ theo đúng trình tự thực hiện này.
Giả mã như sau:
sort jobs by $\uparrow$ order of profit.
permute $P,D$ to match indices.
$X[1,2,\ldots,n] \leftarrow \{0,0,\ldots, 0\}$
for $i \leftarrow 1$ to $n$
$j \leftarrow D[i]$
while $(X[j]\not= 0)$ and $(j \geq 1)$
$j \leftarrow j-1$
if $j \not= 0$
$X[j] \leftarrow i$
Code của thuật toán bằng C:
#define MAX 5000
typedef struct {
int id;
int d;
int p;
} job;
job A[MAX];
int X[MAX];
void greedy_scheduling(int n){
qsort(A, n, sizeof(*A), compare_profit); // sort jobs by increasing order of profit
memset(X, -1, sizeof(X)); // set elements of X to -1
int i = 0, j = 0;
for(i = 0; i < n; i++){
j = A[i].d;
while((X[j]!= -1) && (j > 0)){
j--;
}
if(j > 0) X[j] = i;
}
}
int compare_profit(const void *a, const void *b){
job *c_a = (job *)a;
job *c_b = (job *)b;
return c_b->p - c_a->p;
}
Dễ thấy thuật toán trên có thể được thực thi trong thời gian $O(n^2)$. Trong bài Union-Find, mình sẽ giới thiệu phương pháp sử dụng cấu trúc Union-Find để giảm thời gian xuống còn $O(n\log n)$. Nếu các tác vụ đầu vào đã được sắp xếp theo chiều giảm dần của tiền thưởng, chúng ta còn có thể giảm thời gian xuống còn $O(n \alpha(n))$ trong đó $\alpha(n)$ là hàm Ackerman ngược. Hàm $\alpha(n)$ tăng cực kì chậm và $\alpha(n) \leq 5$ với mọi giá trị thực tế của $n$. Do đó có thể coi $O(n\alpha(n))$ xấp xỉ $O(n)$.
Vấn đề còn lại là chứng minh rằng thuật toán tham lam cho lời giải tối ưu.
Chứng minh: Chúng ta sẽ chứng minh theo các bước đã chỉ ra ở trên. Gọi $X = \{x_1,x_2,\ldots, x_k\}$ là tập các tác vụ đầu ra của thuật toán tham lam, sắp xếp theo chiều giảm dần cuả tiền thưởng. Gọi $Y = \{y_1,y_2,\ldots, y_m\}$ là tập các tác vụ tối ưu, sắp xếp như $X$. Các tác vụ có phần thưởng bằng nhau trong $Y$ sẽ được sắp xếp ưu tiên theo thứ tự trong $X$. Ví dụ $Y$ chứa $3$ tác vụ $3,4,5$ mà $P[3] = P[4] = P[5]$, trong đó $P[5], P[4]$ xuất hiện trong $X$ và tác vụ $5$ được chọn trước $4$ trong $X$ thì ta sắp xếp chúng theo thứ tự $5,4,3$ trong $Y$.
Nếu $X \subseteq Y$, ta suy ra $X = Y$ vì nếu không, thuật toán tham lam sẽ chọn thêm ít nhất một phần tử nữa vào $X$. Chọn $Y$ sao cho $X \cap Y$ là lớn nhất. Gọi $i$ là chỉ số nhỏ nhất sao cho $y_i \not= x_i$. Ta có $P[y_i] \leq P[x_i]$ vì nếu không thuật toán tham lam sẽ chọn $y_i$. Theo cách sắp xếp $Y$, ta suy ra $x_i \not\in Y$.
Giả sử tồn tại một tác vụ $ y \subseteq Y - X$ có thời hạn sớm hơn hoặc bằng $x_i$. Nếu $P[y] \leq P[x_i]$, ta có thể đổi chỗ $y$ và $x_i$, qua đó thu được phản chứng theo như lập luận ở trên. Do đó, $P[y] > P[x_i]$, nhưng điều đó có nghĩa là $y \in X$. Suy ra, không có tác vụ nào trong $Y - X$ có thời hạn sớm hơn hoặc bằng $x_i$.
Gọi $y'_1,y'_2,\ldots, y'_m$ là một lịch trình thực thi các tác vụ trong $Y$ và gọi $t$ là số nhỏ nhất sao cho $y'_t \not\in X$. Do đó, theo như lập luận ở trên, ta có $D[y'_t] \geq D[x_i]$ và $P[y'_t] \leq P[x_i]$. Vì $\{y'_1, y'_2, \ldots, y_{t-1}', x_i\}$ có một lịch trình thực thi sao cho mọi tác vụ đều trước thời hạn, bằng cách thay thế $y'_t$ bởi $x_i$, ta thu được lời giải tối ưu khác $Y'$ với $|Y' \cap X| > |Y \cap X|$, qua đó thu được phản chứng.
Code: chọn lớp học, lập lịch.
Tham khảo
[1] Jeff Erickson. Greedy Algorithm Lecture Notes, UIUC.
[2] George Kocur, MIT OWC lecture notes, MIT.
[3] Cormen, Thomas H.; Leiserson, Charles E., Rivest, Ronald L., Stein, Clifford.Introduction to Algorithms (2nd ed.) . MIT Press and McGraw-Hill (2001). ISBN 0-262-03293-7.
Tags: greedy algorithm, scheduling
-
Bài toán lập lịch có vấn đề trong chứng minh rồi. Phản ví dụ :
1 100 3
2 80 3
3 1 1Nếu theo trình tự thì đc 180 đồng. Nhưng theo trình tự 3-2-1 thì đc 181 đồng cơ
-
Hi bạn.
Hình như bạn hiểu sai thuật toán. Khi thuật toán chọn một việc để đưa vào tập lời giải, nó sẽ không thực thi ngay. Theo ví dụ của bạn, thuật toán sẽ chọn Job 1 và 2 trước (nhưng nó sẽ không thực thi ngay). Khi xét Job 3, thuật toán sẽ kiểm tra xem có lịch nào để thực thi được cả 1,2,3 hay không (trong trường hợp này là có). Do đó, nó sẽ chọn Job 3 đưa vào lời giải. Cuối cùng kết quả vẫn là 181.Mình trích lại thuật toán: "Trong tập các tác vụ chưa được chọn, chọn tác vụ có tiền thưởng lớn nhất nếu tác vụ này vẫn còn thực thi được. Ở đây ta luôn duy trì một danh sách các tác vụ đã chọn và một tác vụ gọi là thực thi được nếu ta thêm tác vụ này vào danh sách đó, vẫn tồn tại một cách thực thi sao cho tất cả các tác vụ được hoàn thành trước thời hạn"
Hùng
-
Vâng ạ em đã hiểu, em đã đọc kỹ bài này thì duy chỉ có cái chứng minh Theorem 4 em thấy nó hơi tối với khó hiểu một tý, anh có thể xem lại và chỉnh sửa cho nó sáng sủa một tý không ạ. Chẳng hạn chỗ P[y_i] <= P[x_i] rồi suy ra x_i không thuộc Y là chưa chặt chẽ. Nếu dấu bằng xẩy ra P[y_i] = P[x_i] thì có thể có x_i thuộc Y chứ.
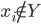
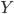
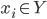
6 comments
Comments feed for this article
Trackback link: http://www.giaithuatlaptrinh.com/wp-trackback.php?p=198